10 Estatística Descritiva
A estatística descritiva é utilizada para descrever e organizar as características básicas dos dados de um estudo. É particularmente útil para descrever a tendência central e a dispersão dos valores, sendo útil para perceber a distribuição dos dados.
Quando finalizar este capítulo, deverá ser capaz de:
10.1 Pacotes e dados necessários
Nesta aula e seguintes, será sempre necessário utilizar o tidyverse para a manipulação de dados:
Do mesmo modo, se ainda não o fez, deverá importar o ficheiro cardiology.xlsx, disponibilizado no material da aula.
10.2 Sumariar dados numéricos
Os dados numéricos são descritos recorrendo a dois tipos de medidas de sumário (Table 10.1):
medidas de tendência central (indicam-nos onde o centro da distribuição de valores de uma dada variável se localiza)
medidas de dispersão (descreve a variação dos valores)
| Medidas de tendência central | Medidas de dispersão |
|---|---|
|
|
10.3 Estatísticas de sumário
Medidas de tendência central
A. Média
Vantagens da média
- Utiliza todos os dados no seu cálculo.
- É definida algebricamente.
Desvantagens da média
- É muito influenciada por valores extremos (outliers), pelo que pode não ser adequada para descrever distribuições assimétricas.
Seja \(x_1, x_2,...,x_{n-1}, x_n\) um conjunto de n medições. A média amostral, \(\bar{x}\), é a soma das observações dividida pelo seu número n, ou seja1:
1 A média populacional representa-se por \(\mu\).
\[ \bar{x}= \frac{x_1 + x_2 + ... + x_{n-1} + x_n}{n} = \frac{1}{n}\sum_{i=1}^{n}x_{i} \] onde \(x_{i}\) representa os valores de cada observação individual e \({\sum_{i=1}^{n}x_{i}}\) a sua soma.
Utilizando a tabela de dados cardiology, a média amostral das idades dos pacientes (guardada na variável age) pode ser calculada através da função mean()2:
2 Se existirem valores omissos (NA), como é o caso, o argumento na.rm = TRUE exclui os valores omissos do cálculo. Caso não remova os valores omissos, o resultado retornará NA, uma vez que todas as operações aritméticas envolvendo NA resultam em NA.
mean(cardiology$age, na.rm = TRUE)[1] 48.67059Este problema também poderia ser resolvido recorrendo a funções do tidyverse. Embora, neste caso, não seja necessário (e, de facto, acabe mesmo por tornar o código mais complexo), vamos utilizar este exemplo para introduzir dois novos conceitos que lhe serão úteis no futuro: a função summarise() e o pipe (%>%).
Primeiro, veja como este problema seria resolvido recorrendo ao Tidyverse:
Note que há algumas diferenças:
- Não escrevemos
cardiology$agepara indicarmos ao R que pretendíamos fazer a média da variávelagedentro do objetocardiology; - Apareceu o
%>%(conhecido como pipe, lê-se “paipe”), que nunca tínhamos utilizado; - E utilizamos a função
mean()dentro da funçãosummarise().
Pipe (%>%)
O operador Pipe (%>%) é um operador muito útil para melhorar a legibilidade do código em R, permitindo passar o que está à esquerda do pipe para o que está à direita. Quando lemos o código, o operador Pipe (%>%) pode ler-se, literalmente, como “e depois”.
No caso em apreço, o que temos é:
- Chamar o objeto “cardiology”; e depois… (
%>%) - Sumariar o objeto, calculando a média da variável “age”.
A grande vantagem do Pipe (%>%) é que permite encadear múltiplas operações sem prejudicar a legibilidade do código, como veremos em exemplos seguintes.
Função summarise()
A função summarise(), por si só, não é particularmente útil (i.e., não serve de nada fazer summarise(age)). Deve ser sempre conjugada com outras funções de estatística descritiva. Neste caso, como pretendíamos calcular a média, utilizamos a função mean().
Note que se escreveu summarise(mean = mean(age)). A segunda parte, mean(age), é a parte responsável pelo cálculo da média da variável age do objeto cardiology (o R sabe que se trata da variável age do objeto cardiology porque escrevemos isso utilizando o Pipe %>%). A primeira parte, mean =, tem como único objeto dar o nome mean ao resultado, no output da função, para facilitar a leitura do output. Note que poderíamos ter escrito:
ou poderíamos mesmo não ter escrito nada:
# A tibble: 1 × 1
`mean(age, na.rm = TRUE)`
<dbl>
1 48.7A lista de funções que pode utilizar com o summarise() é extensa, e inclui:
B. Mediana
A mediana é uma medida de tendência central alternativa, menos sensível a valores extremos. A mediana calcula-se ordenando todos os valores observados (em ordem crescente ou decrescente) e selecionando o valor que se encontra exatamente no ponto médio. Se o número de observações n for ímpar, a mediana é exatamente o valor central. Se o número de observações for par, a mediana corresponde à média entre os dois valores centrais.
Vantagens da mediana
- Não é afetada por valores extremos.
Desvantagens da mediana
- Não toma em conta o valor exato de toda e cada observação e, por isso, não usa toda a informaçaõ disponível nos dados.
- Não é definida algebricamente.
Por isso, a mediana, md, de n observações é dada por:
o valor número \(\frac{n+1}{2}\), \(md=x_{\frac{n+1}{2}}\), se n for ímpar.
a média dos valores \(\frac{n}{2}\) e \(\frac{n+1}{2}\), \(md=\frac{1}{2}(x_{\frac{n}{2}}+x_{\frac{n+1}{2}})\), se n for par.
Medidas de Dispersão
A. Variância
A variância amostral, \(s^2\), é uma medida de dispersão dos dados. Calcula-se fazendo a soma dos quadrados dos desvios em relação à média amostral e dividindo por \(n\)3
3 A variância na população representa-se por \(\sigma^2\). Como verá em aula teórica, a estimativa da variância na população representa-se por \(\hat{\sigma}^2\) e calcula-se com base nos dados amostrais: \(\hat{\sigma}^2 = \frac{\sum\limits_{i=1}^n (x -\bar{x})^2}{n-1}\).
\[s^2 = \frac{\sum\limits_{i=1}^n (x -\bar{x})^2}{n}\]
A variância expressa-se em unidades ao quadrado, pelo que não é facilmente interpretável.
B. Desvio padrão
O desvio padrão (s) de uma amostra corresponde à raiz quadrada da variância4
4 O desvio padrão na população representa-se por \(\sigma\). Como verá em aula teórica, a estimativa do desvio padrão na população representa-se por \(\hat{\sigma}\) e calcula-se com base nos dados amostrais: \(\hat{\sigma} = \frac{\sum\limits_{i=1}^n (x -\bar{x})}{n-1}\).:
\[s = \sqrt{s^2} = \sqrt\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})^2}{n-1}\]
Ao contrário da variância, o desvio padrão expressa-se nas mesmas unidades dos valores originais.
C. Âmbito/Amplitude
O âmbito ou amplitude é a diferença entre o valor mais pequeno (mínimo) e maior (máximo). No R, a função range() retorna um vetor que contém os valores mínimo e máximo:
Uma desvantagem de utilizar o âmbito como medida de dispersão é que este é sensível a valores extremos.
range(cardiology$age, na.rm = TRUE)[1] 18 83A diferença entre os dois valores, 83 - 18, é:
Alternativamente, também poderia ter obtido diretamente os valores mínimo e máximo, recorrendo às funções min() e max(), respetivamente:
D. Âmbito/Amplitude Interquartil
O âmbito/amplitude interquartil corresponde à diferença entre o terceiro e o primeiro quartil (respetivamente, os percentis 75 e 25). Pode obter o âmbito utilizando a função IQR():
O âmbito interquartil apresenta a vantagem de não ser sensível a valores extremos.
IQR(cardiology$age, na.rm = TRUE)[1] 21Também pode obter diretamente os quartis, utilizando a função quantile():
quantile(cardiology$age, prob=0.25, na.rm = T) # 1.º Quartil (Percentil 25)25%
38 quantile(cardiology$age, prob=0.75, na.rm = T) # 3.º Quartil (Percentil 75)75%
59 25% 75%
38 59 Note que a mediana não é mais do que o percentil 50:
quantile(cardiology$age, prob=0.50, na.rm=T)50%
48 Agora que aprendeu um conjunto alargado de medidas de sumário, vamos calcular todas ao mesmo tempo:
cardiology %>%
summarise(
n = n(),
na = sum(is.na(age)), # Calcula o número de valores omissos
min = min(age, na.rm = TRUE),
q1 = quantile(age, 0.25, na.rm = TRUE),
median = median(age, na.rm = TRUE),
q3 = quantile(age, 0.75, na.rm = TRUE),
max = max(age, na.rm = TRUE),
mean = mean(age, na.rm = TRUE),
sd = sd(age, na.rm = TRUE),
)# A tibble: 1 × 9
n na min q1 median q3 max mean sd
<int> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 428 3 18 38 48 59 83 48.7 14.1summarise()
Como pode ter notado, uma das vantagens da função summarise() é que permite conjugar várias funções para sumariar dados. As funções são separadas por vírgulas (,). Note que, no código acima, foi utilizada a tecla Enter para escrever o código em linhas separadas e facilitar a leitura.
B. Estatísticas de sumário por grupo
Muitas vezes, terá interesse em calcular estatísticas de sumário separadamente por grupo. Comecemos por ver, como exemplo, como se calcularia a média da idade separadamente para homens e mulheres:
# A tibble: 2 × 2
sex mean
<chr> <dbl>
1 female 47.6
2 male 49.9group_by() conjugada com função summarise()
A função group_by() é uma função do tidyverse/dplyr, que serve para agrupar dados por uma ou mais variáveis antes de lhe ser aplicada uma outra função, como a função summarise(). No caso em apreço, o código pode ser interpretado como:
- Chamar o objeto “cardiology”; e depois… (
%>%) - Agrupar por sexo (“sex)”; e depois… (
%>%) - Sumariar, calculando a média da variável “age”.
De facto, se quiser, pode calcular várias medidas de sumário agrupadas por sexo e guardar os resultados num novo objeto:
summary_age_sex <- cardiology %>%
group_by(sex) %>%
summarise(
n = n(),
na = sum(is.na(age)), # Calcula o número de valores omissos
min = min(age, na.rm = TRUE),
q1 = quantile(age, 0.25, na.rm = TRUE),
median = median(age, na.rm = TRUE),
q3 = quantile(age, 0.75, na.rm = TRUE),
max = max(age, na.rm = TRUE),
mean = mean(age, na.rm = TRUE),
sd = sd(age, na.rm = TRUE),
)
summary_age_sex# A tibble: 2 × 10
sex n na min q1 median q3 max mean sd
<chr> <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 female 237 2 19 36 47 58.5 83 47.6 14.5
2 male 191 1 18 41 49 59 80 49.9 13.5
10.4 Visualizar Dados Numéricos
A. Histograma
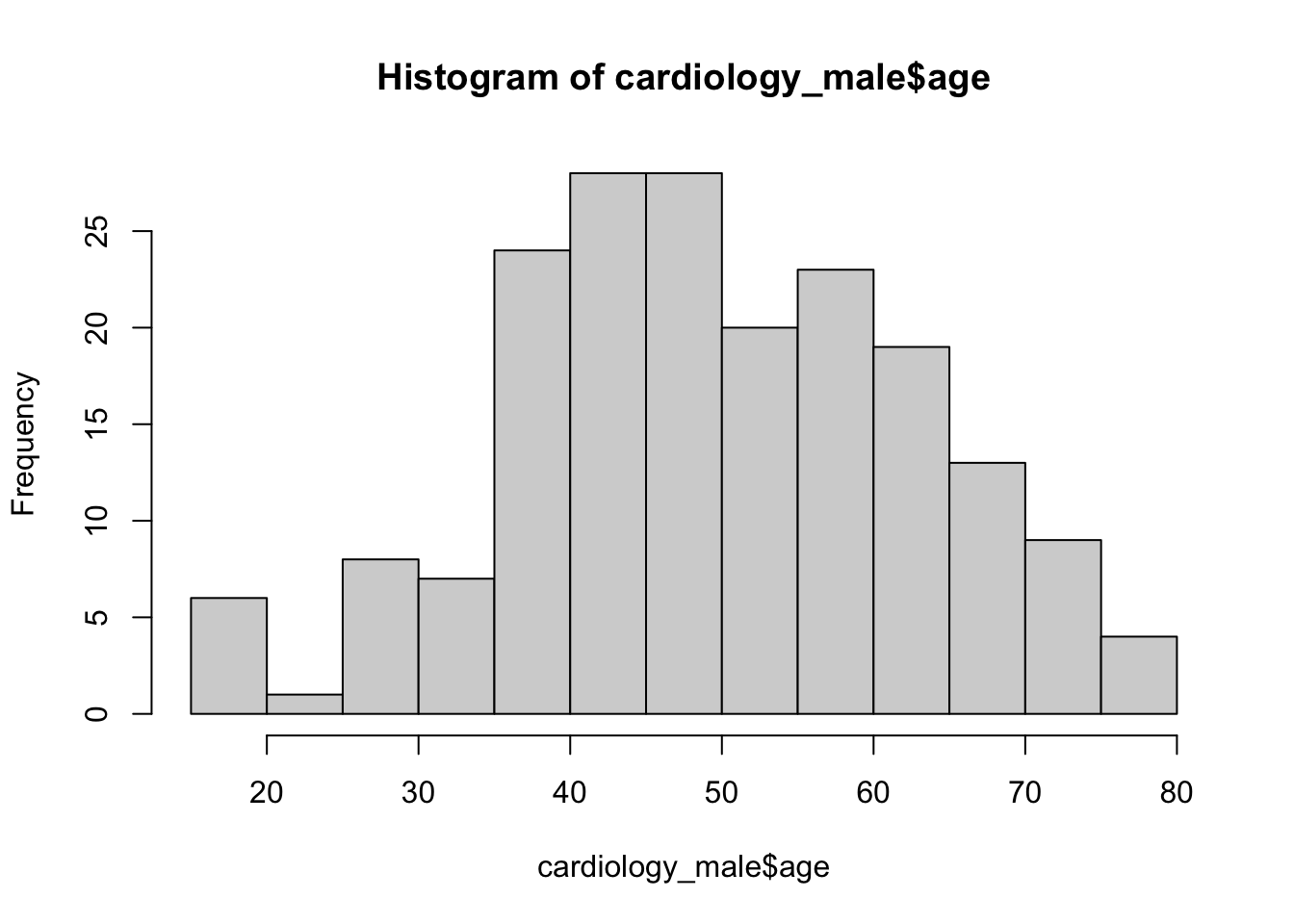
A forma mais comum para representar uma distribuição de frequências de uma variável numérica contínua é recorrendo ao histograma. Os histogramas (Figure 10.1) mostram a distribuição dos dados como uma série de barras sem espaçamento entre elas. Cada barra representa um intervalo de valores. A altura das barras indica sobre a frequência das observações. São particularmente úteis para avaliar a simetria da distribuição dos dados.
hist(cardiology$age, breaks = 15, main = "Distribuição de Idades", xlab = "Idade", ylab = "Frequência")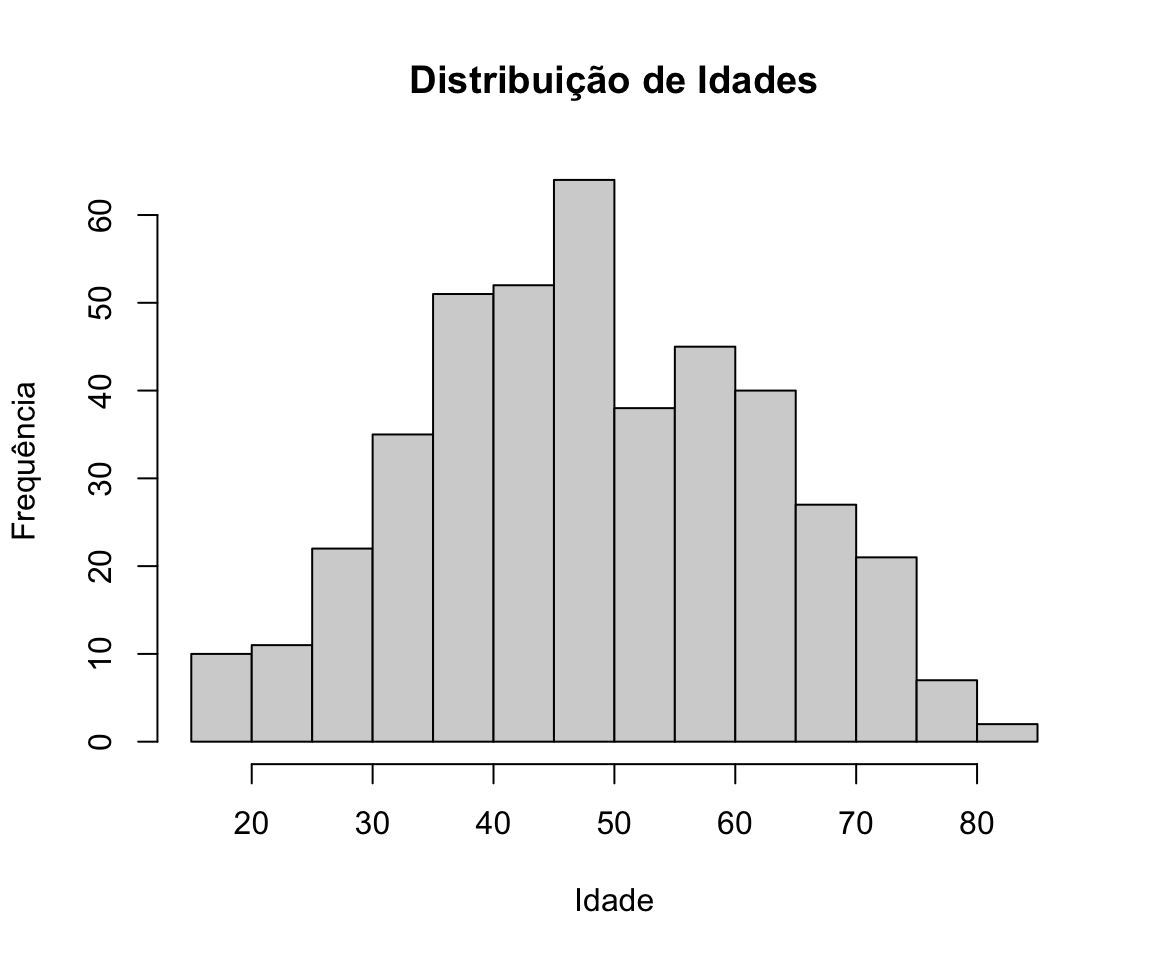
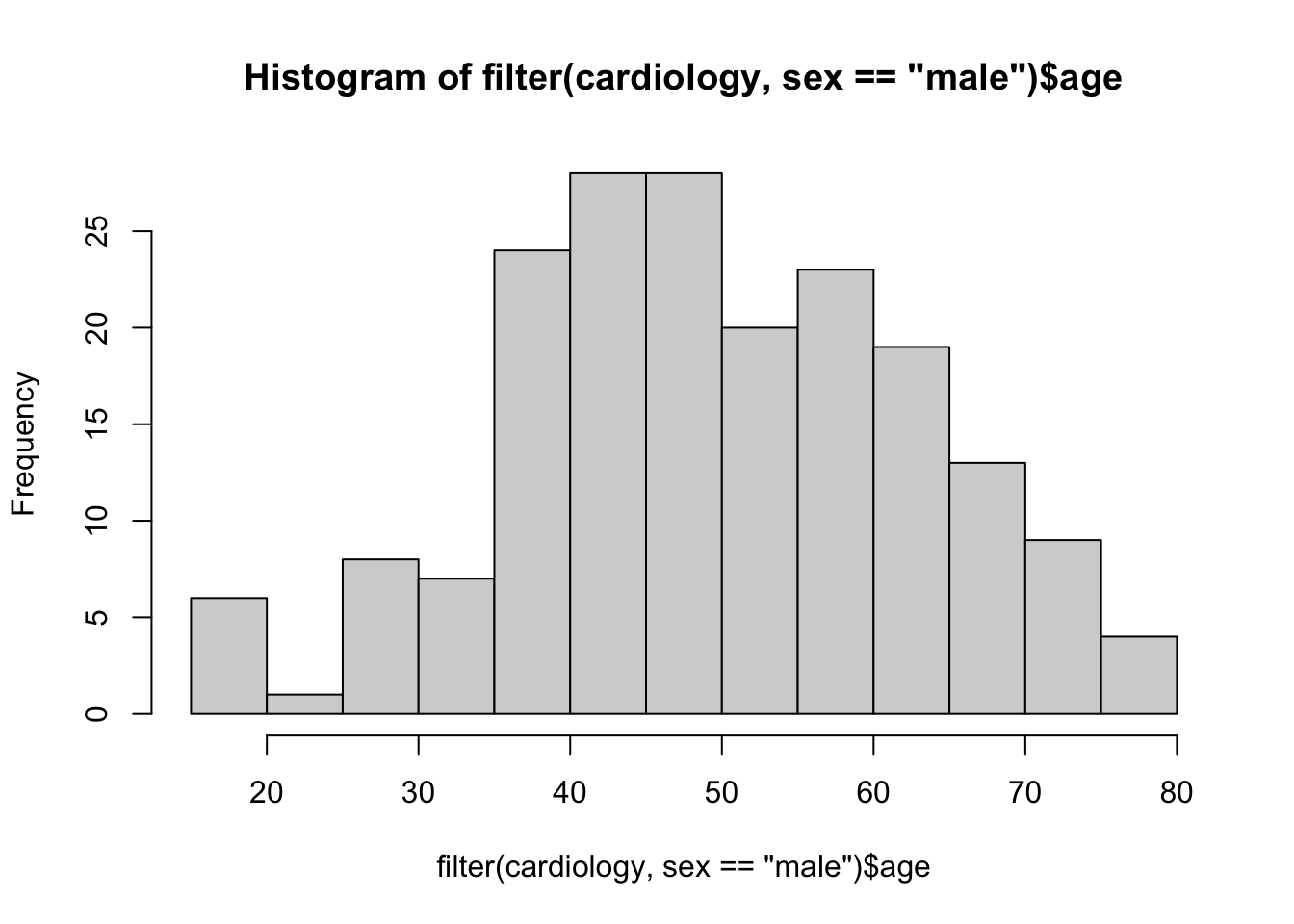
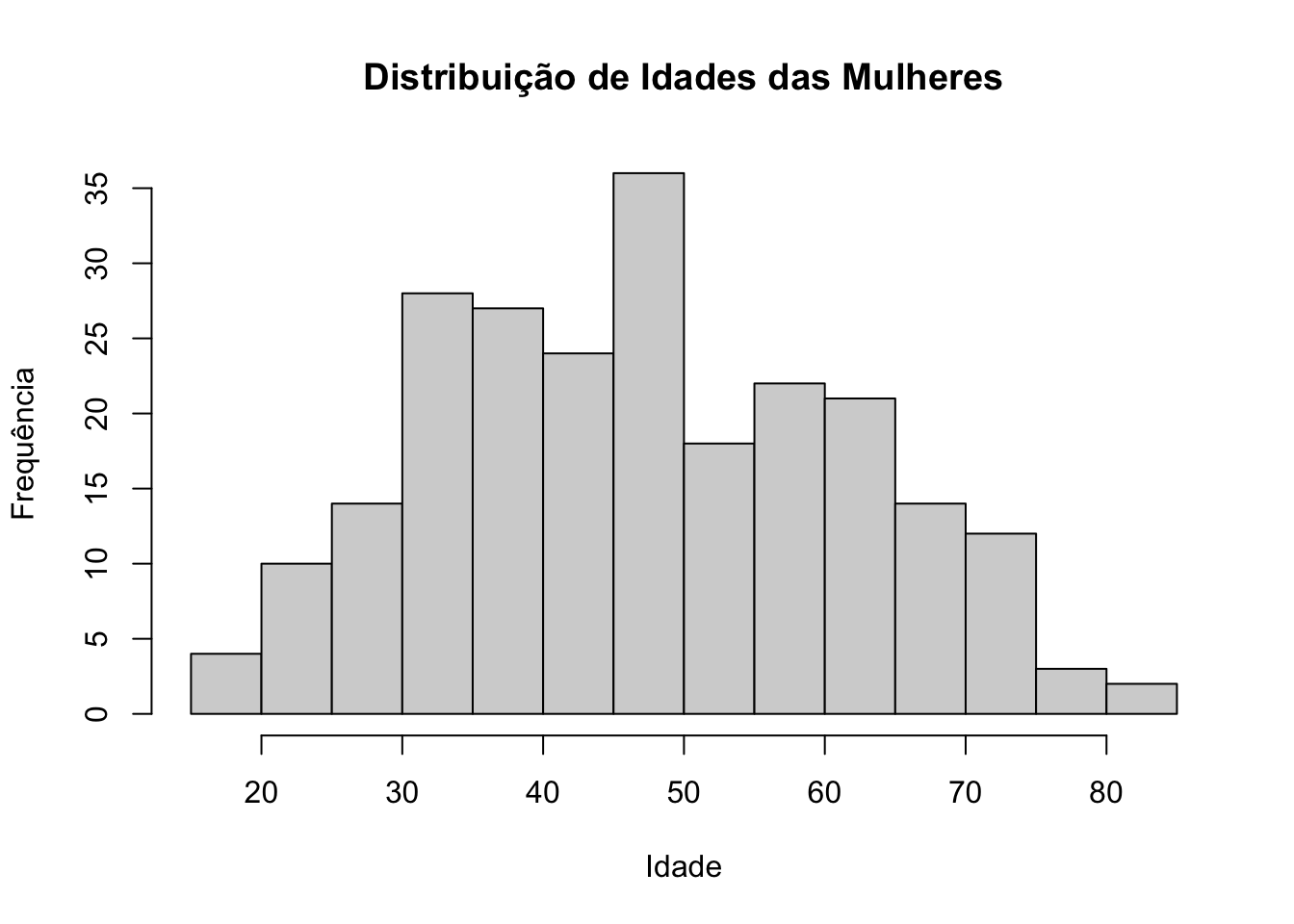
Também é possível fazer histogramas (e outros gráficos) separadamente para diferentes grupos, embora neste caso não seja possível recorrer à função group_by(). Por exemplo, para fazer um histograma de idades apenas para os indivíduos do sexo masculino, pode utilizar a função filter() e a sintaxe é:
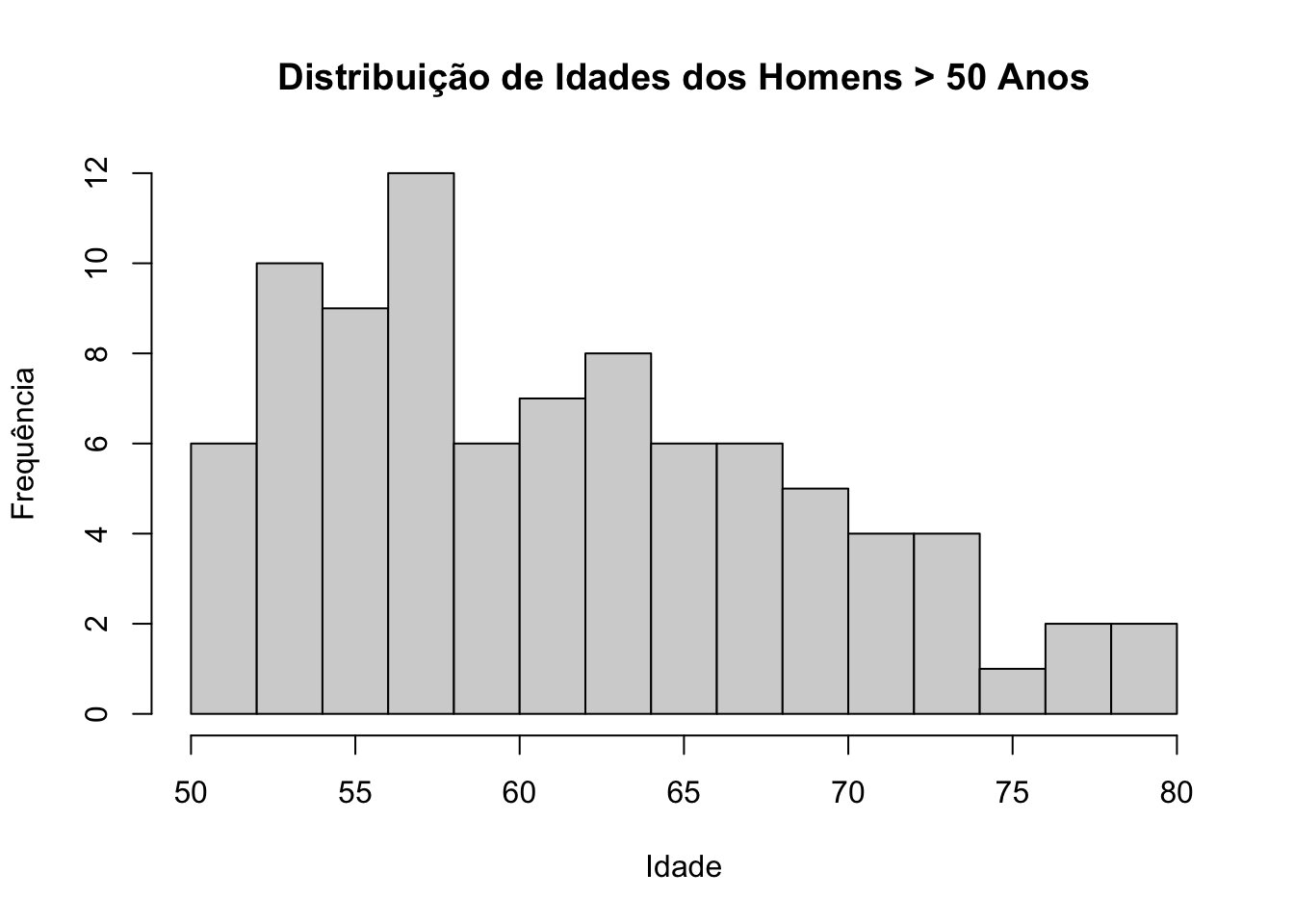
hist(filter(cardiology, sex == "male")$age, breaks = 15, main = "Distribuição de Idades dos Homens", xlab = "Idade", ylab = "Frequência")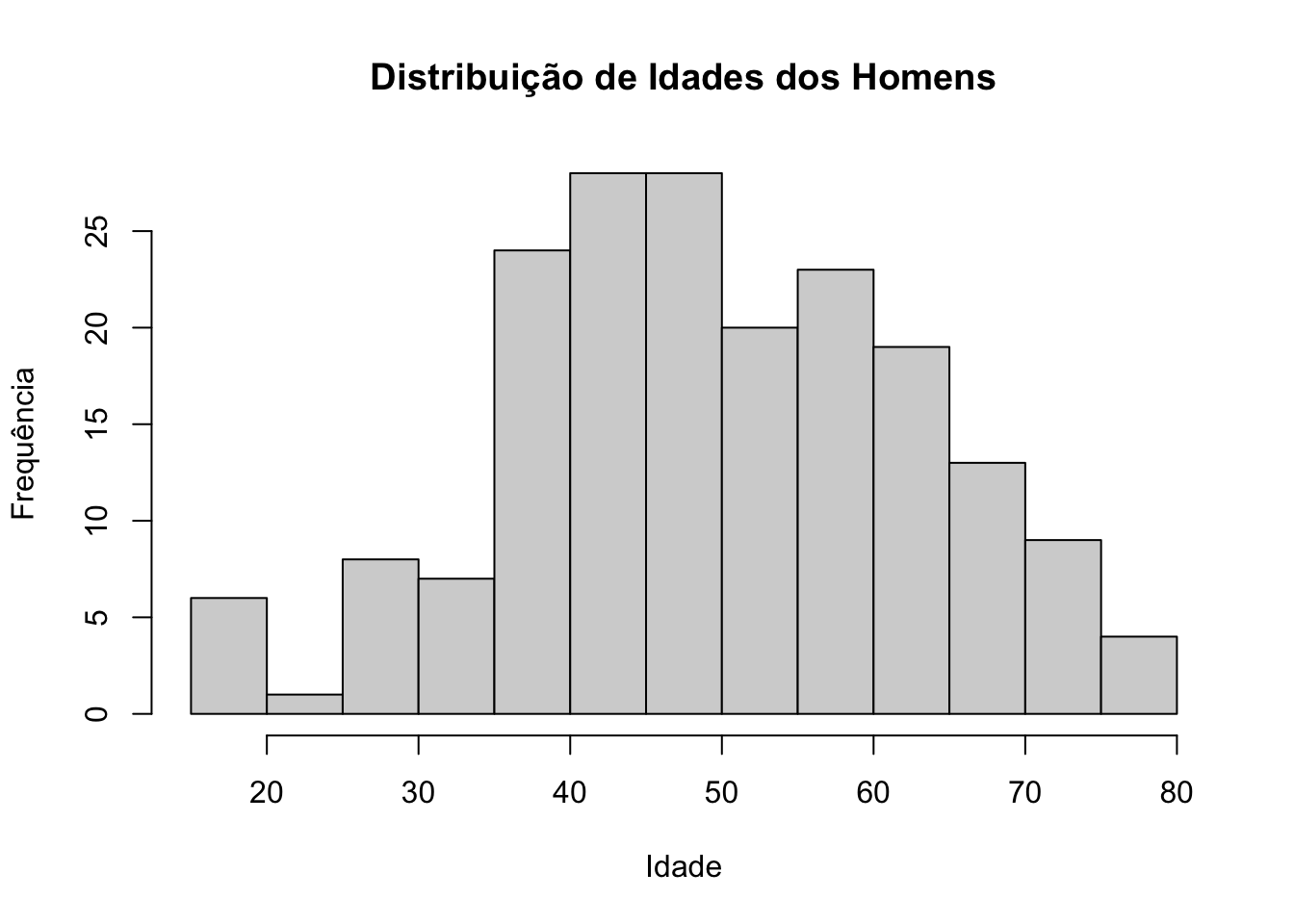
filter()
A função filter() é uma função dependente do tidyverse que pode ser utilizada para criar um novo data frame a partir do data frame original, o qual é filtrado de acordo com uma condição especificada.
filter(cardiology, sex == "male")# A tibble: 191 × 7
age sex height weight QRS HR LOS
<dbl> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 75 male 190 80 91 71 5
2 54 male 172 95 138 76 8
3 55 male 175 94 115 77 7
4 NA male 190 80 88 81 5
5 44 male 168 56 84 79 5
6 62 male 170 72 152 74 9
7 30 male 170 73 133 76 8
8 47 male 171 59 82 83 5
9 73 male 165 63 91 87 5
10 45 male 169 67 90 86 5
# ℹ 181 more rowsComo pode verificar, a função filter() toma dois argumentos:
- o primeiro argumento corresponde ao nome do data frame que pretendemos filtrar (neste caso, o objeto
cardiology); - o segundo data frame corresponde à condição que pretendemos impor ao fitro. Neste caso, queremos fazer um histograma de idades para o sexo masculino. O data frame
cardiologytem uma variável relativa ao sexo (sex) e, como vimos anteriormente, esta variável é do tipo character string e pode tomar um de dois valores:maleoufemale. Uma vez que o objetivo é filtrar apenas as observações do sexo masculino, temos de definirsex == "male". As aspas (") são necessárias por se tratarem de dados de texto (character string). O duplo sinal de igual (==) é necessário porque é o operador relacional de igualdade no R. Recorde que o sinal de igual simples (=) é um operador de atribuição equivalente ao<-.
No caso acima, o código filter(cardiology, sex == "male") retorna um data frame unicamente com as linhas de indivíduos do sexo masculino. Se preferir, pode mesmo guardar este data frame num novo objeto:
cardiology_male <- filter(cardiology, sex == "male")
cardiology_male# A tibble: 191 × 7
age sex height weight QRS HR LOS
<dbl> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 75 male 190 80 91 71 5
2 54 male 172 95 138 76 8
3 55 male 175 94 115 77 7
4 NA male 190 80 88 81 5
5 44 male 168 56 84 79 5
6 62 male 170 72 152 74 9
7 30 male 170 73 133 76 8
8 47 male 171 59 82 83 5
9 73 male 165 63 91 87 5
10 45 male 169 67 90 86 5
# ℹ 181 more rowsNote que é possível aceder aos valores de idade utilizando, como habitualmente, o sinal $ para acedermos à coluna age do data frame:
filter(cardiology, sex == "male")$age [1] 75 54 55 NA 44 62 30 47 73 45 44 49 53 69 50 45 39 52 42 46 37 34 45 57 51
[26] 63 19 40 68 55 51 27 63 46 50 43 29 74 50 72 71 58 61 46 56 46 40 47 35 49
[51] 34 36 18 32 36 45 59 54 24 40 44 50 56 66 18 44 57 61 62 65 46 33 53 62 47
[76] 18 63 53 50 77 42 56 67 37 43 36 72 80 57 45 43 56 43 46 48 58 46 59 68 53
[101] 45 48 44 43 61 31 41 49 57 73 65 57 45 40 55 51 59 74 67 37 53 40 41 80 69
[126] 70 64 57 52 55 37 26 54 38 67 59 65 42 37 42 54 48 72 36 20 62 64 26 45 47
[151] 47 56 54 40 57 46 43 59 64 30 48 67 66 57 36 47 35 78 44 70 36 59 47 57 64
[176] 41 30 65 51 36 58 64 47 70 20 37 37 29 45 37 36O código acima retorna um conjunto de valores que correspondem à idade dos indivíduos do sexo masculino. Consequentemente, para fazer um histograma, basta envolver o código acima na função hist():
Opcionalmente, poderá depois definir os argumentos main, xlab, ylab e breaks para personalizar o histograma.
Se optar por guardar o data frame filtrado num novo objeto cardiology_male, pode fazer as operações sobre este novo objeto, mas isso não é necessário:
hist(cardiology_male$age)
Para fazer o histograma para o sexo feminino, bastaria depois alterar o filtro para female:
Os operadores relacionais são utilizados para fazer comparações no R. No exemplo anterior, vimos o operador relacional de igualdade (==). Eis uma lista dos operadores relacionais disponíveis no R (Table 10.2):
| símbolo | lê-se como |
|---|---|
| < | menor do que |
| > | maior do que |
| == | igual a |
| <= | menor ou igual a |
| >= | maior ou igual a |
| != | diferente de |
Assim, por exemplo, se pretendesse fazer um histograma de idades incluindo apenas os indivíduos com mais do que 50 anos, deveria escrever age > 50:
hist(filter(cardiology, age > 50)$age, breaks = 15, main = "Distribuição de Idades > 50 Anos", xlab = "Idade", ylab = "Frequência")
É inclusivamente possível combinar diferentes comparações recorrendo a operadores lógicos (Table 10.3):
| símbolo | lê-se como |
|---|---|
| & | e |
| | | ou |
| ! | não |
Assim, se pretender fazer um histograma de idades para os homens com mais do que 50 anos:
B. Box Plot
Os box plots (ou, em Português, gráfico em caixa de bigodes) são úteis para sumariar a distribuição de dados contínuos. Este tipo de gráfico utiliza linhas e caixas para representar distribuições (Figure 10.2):
- A caixa representa o âmbito interquartil, isto é, os limites inferior e superior da caixa representam os percentis 25 e 75. A linha central da caixa representa o percentil 50, que corresponde à mediana.
- Os bigodes são as linhas que partem da caixa. Representam o âmbito das observações, excluindo valores extremos.
- Os pontos que se encontram para lá dos bigodes correspondem a valores extremos. No exemplo abaixo, não existem valores extremos.5
5 Tipicamente, considera-se uma observação como sendo um valor extremo se estiver fora do seguinte intervalo: \[(Q_1 - 1.5 \times IQR, \ Q_3 + 1.5 \times IQR)\]
boxplot(cardiology$age, main = "Distribuição de Idades", ylab = "Idade")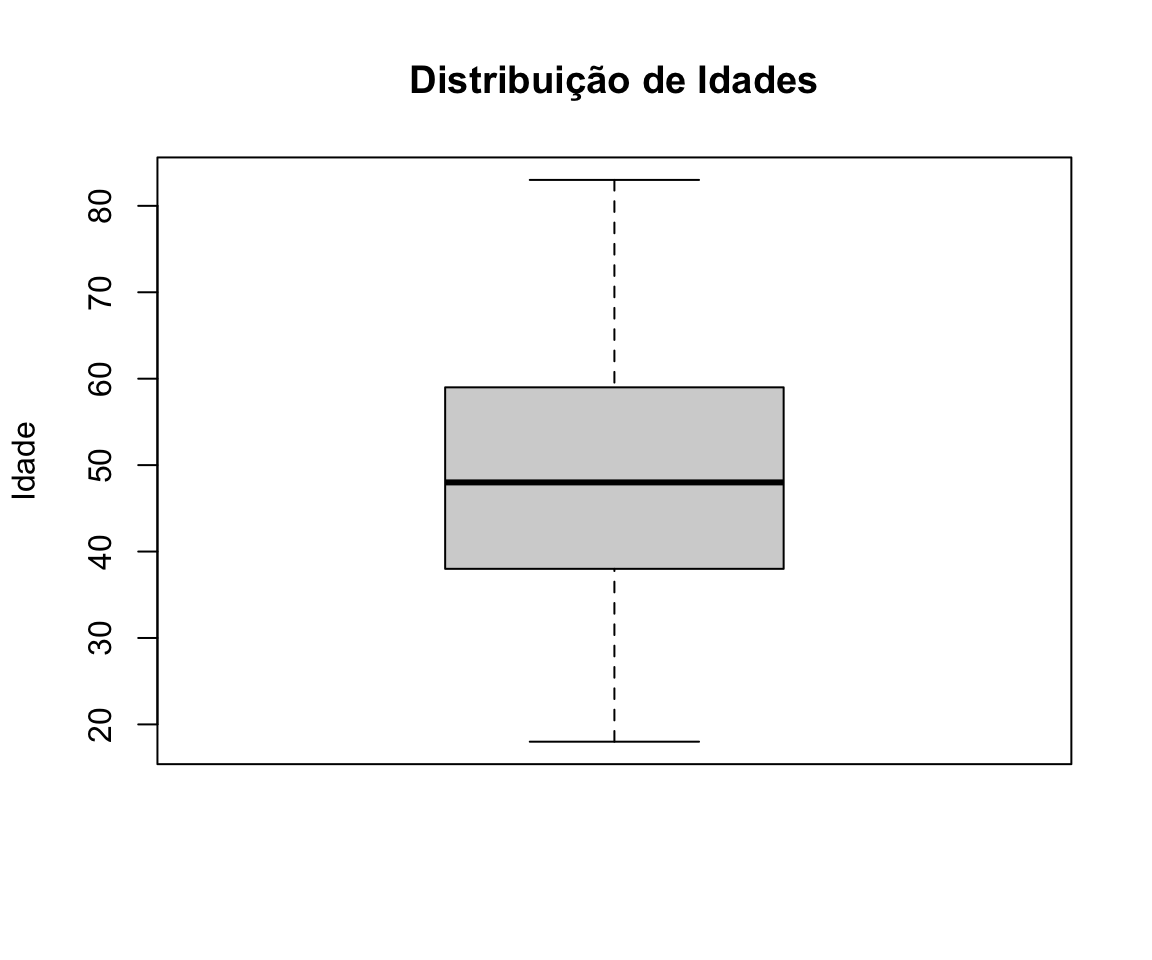
10.5 Sumariar dados categóricos
Para descrever dados categóricos, a melhor forma é apresentar a frequência com que cada categoria ocorre. Essa frequência pode ser expressa em termos absolutos (frequência absoluta) ou relativos (frequência relativa).
A. Frequência absoluta
É possível obter uma tabela de frequências absolutas da variável sex:
A função table() cria uma tabela de frequências absolutas se lhe for passado um vetor (que neste caso corresponde à coluna sex do data frame cardiology). A solução utilizando a sintaxe group_by() %>% summarise() é também bastante elegante: em primeira instância, agrupam-se os dados pela variável categórica que se pretende sumariar (sex) e de seguida contam-se as ocorrências de cada categoria utilizando a função n().
B. Frequência relativa
Do mesmo modo, é possível obter as frequências relativas da variável sex:
A função prop.table() aplicada à função table() cria uma tabela de frequências relativas. A solução utilizando a sintaxe group_by() %>% summarise() é semelhante àquela vista para as frequências absolutas, mas, desta feita, ao invés de nos limitarmos a contar o número de ocorrências de cada categoria, dividimos esse número pelo número total de linhas do data frame (dado pela função nrow()), o que permite obter a frequência relativa de cada categoria.
10.6 Visualizar Dados Categóricos
A. Gráfico de Barras
Para representar graficamente variáveis categóricas, o gráfico de barras é o gráfico de eleição. Para obter adequadamente um gráfico de barras no R, é necessário passar à função barplot() uma tabela de frequências adequada (realizada com recurso à função table(), para frequências absolutas, ou prop.table(), para frequências relativas) (Figure 10.3).
barplot(prop.table(table(cardiology$sex)), main = "Distribuição de sexo", xlab = "Sexo", ylab = "Frequência relativa")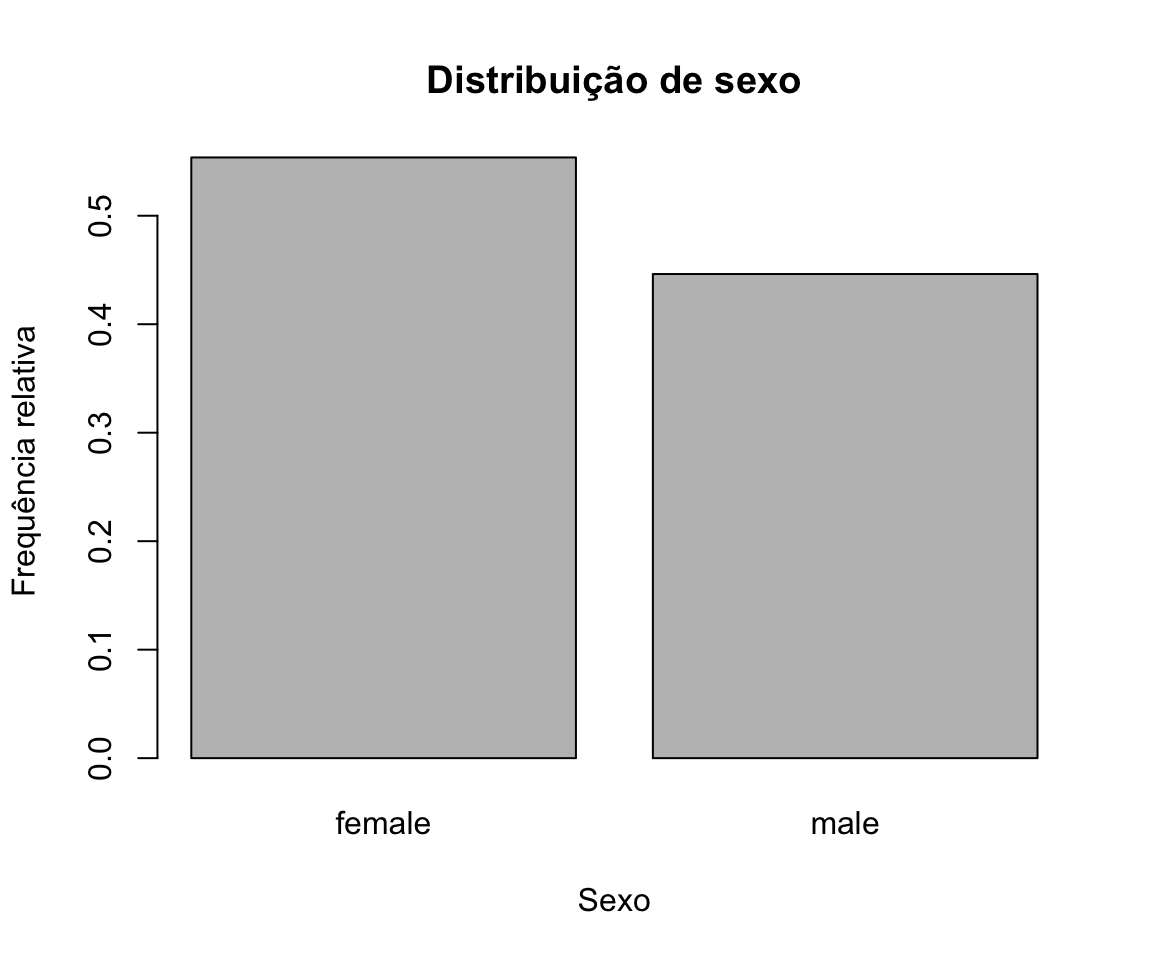
B. Gráfico circular
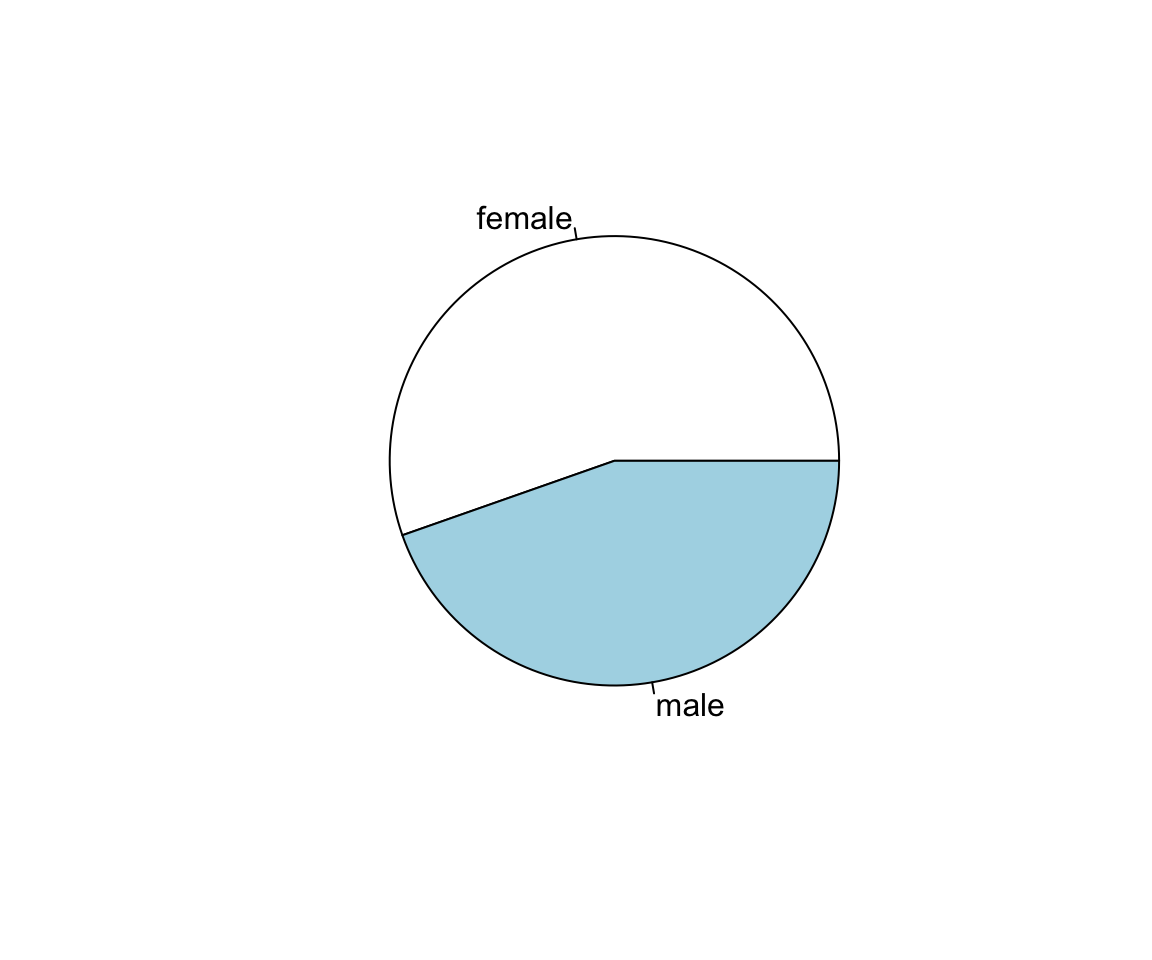
Uma outra opção para representar variáveis categóricas são os gráficos circulares. A sintaxe para criar um gráfico circular é muito semelhante aos gráficos de barras. Neste caso, deve passar a função pie() a uma tabela de frequências adequada (realizada com recurso à função table(), para frequências absolutas, ou prop.table(), para frequências relativas) (Figure 10.4).
10.7 Criar variáveis
Este tema, embora menos relacionado com o tópico da estatística descritiva, é de extrema importância porque, na análise estatística, é frequentemente necessário criar variáveis novas a partir de variáveis pré-existentes. Para isso, poderá recorrer à função mutate(), incluída no tidyverse/dplyr.
Por exemplo, na tabela de dados cardiology, existe uma variável referente à altura (height), onde a altura está guardada em centímetros. Poderia ser do nosso interesse converter a altura em metros:
# A tibble: 428 × 8
age sex height weight QRS HR LOS height_m
<dbl> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 75 male 190 80 91 71 5 1.9
2 56 female 165 64 81 66 5 1.65
3 54 male 172 95 138 76 8 1.72
4 55 male 175 94 115 77 7 1.75
5 NA male 190 80 88 81 5 1.9
6 40 female 160 52 77 59 5 1.6
7 49 female 162 54 78 98 5 1.62
8 44 male 168 56 84 79 5 1.68
9 50 female 167 67 89 59 5 1.67
10 62 male 170 72 152 74 9 1.7
# ℹ 418 more rowsNote a existência de uma nova variável, height_m, no final do data frame, que tem agora 8 colunas.
Analisando em detalhe:
- A função
mutate()tem sempre a formamutate(nova_variável = ...). Ou seja, antes do=deve escrever o nome da nova variável (à sua escolha, neste casoheight_m); e depois do=, deve escrever o conteúdo da nova variável ou como é que o R pode calcular esse conteúdo. Neste caso, escrevemos que o R deve dividir a variávelheightpor100. - Antes do Pipe (
%>%), temos o nome do objeto (cardiology) para, como habitual, indicar ao R que é para “pegar” no objetocardiologye depois (%>%) aplicar a funçãomutate(). - Por fim, temos de guardar o resultado desta operação. Neste caso, estamos a guardá-lo num objeto chamado
cardiology(com o mesmo nome do objeto original), mas poderíamos guardar num objeto com um nome diferente caso pretendêssemos manter as duas versões do data frame.
Quando cria uma nova variável, é recomendado que utilize um nome diferente da variável original. Assim, caso cometa algum erro, pode refazer a operação utilizando a variável original. Pelo contrário, caso guardasse a nova variável com o mesmo nome da variável original (e consequentemente substituindo o conteúdo da variável original), perderia toda a informação em caso de erro.
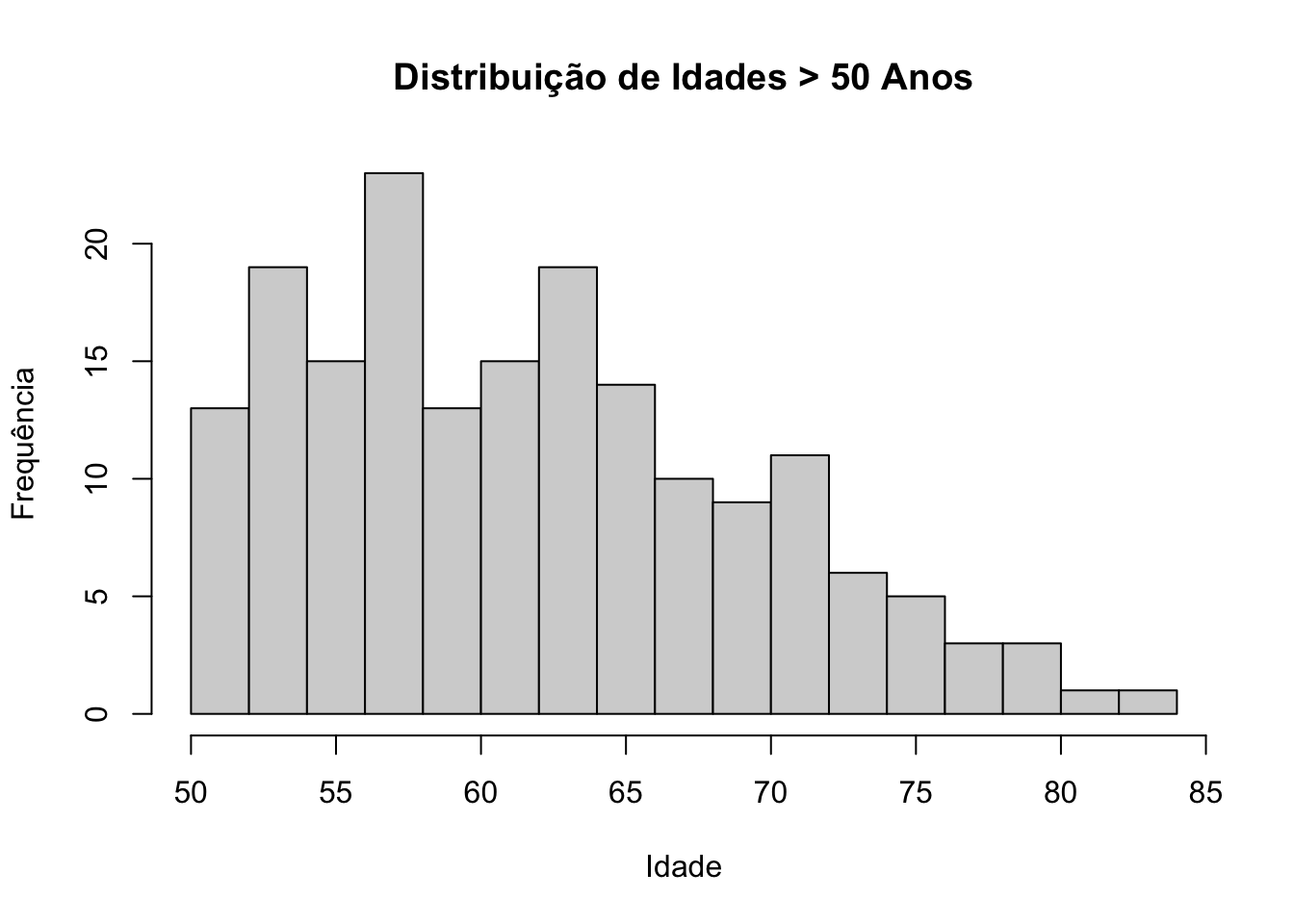
Também é útil que aprenda a categorizar variáveis contínuas. Por exemplo, poderia ter interesse em dicotomizar a variável idade em “indivíduos com mais de 50 anos” (over50) e “indivíduos com 50 anos ou menos” (under50). Para isso, deve conhecer a função ifelse():
# A tibble: 428 × 9
age sex height weight QRS HR LOS height_m age_bin
<dbl> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <chr>
1 75 male 190 80 91 71 5 1.9 over50
2 56 female 165 64 81 66 5 1.65 over50
3 54 male 172 95 138 76 8 1.72 over50
4 55 male 175 94 115 77 7 1.75 over50
5 NA male 190 80 88 81 5 1.9 <NA>
6 40 female 160 52 77 59 5 1.6 under50
7 49 female 162 54 78 98 5 1.62 under50
8 44 male 168 56 84 79 5 1.68 under50
9 50 female 167 67 89 59 5 1.67 under50
10 62 male 170 72 152 74 9 1.7 over50
# ℹ 418 more rowsNote a existência de uma nova variável, age_bin, no final do data frame.
Analisando em detalhe:
- Toda a sintaxe até ao
=na funçãomutatepermanece semelhante ao exemplo anterior:cardiology <- cardiology %>% mutate(age_bin =. Portanto, estamos a “pegar” no objetocardiologye criar uma nova variávelage_binrecorrendo à funçãomutate(). Depois, estamos a guardar no objetocardiology. - A novidade vem depois do
=. Recorde-se que, na funçãomutate(), o que aparece depois do=são as instruções dadas ao R para criar uma nova variável. Neste caso, estamos a utilizar a funçãoifelse(), que apresenta três argumentos:- O primeiro argumento corresponde necessariamente a uma condição utilizando um operador relacional. Neste caso, a condição
age > 50. - O segundo argumento corresponde à instrução sobre o que deve acontecer quando a condição é verdadeira (
TRUE). Neste caso, quandoage > 50, a nova variávelage_binassume o valor textual (note as aspas")over50. - O terceiro argumento corresponde à instrução sobre o que deve acontecer quando a condição é falsa (
FALSE). Neste caso, quandoagenão é>50, ou seja, quando a idade for igual ou inferior a 50, a nova variávelage_binassume o valor textualunder50.
- O primeiro argumento corresponde necessariamente a uma condição utilizando um operador relacional. Neste caso, a condição
Isto permite-lhe criar uma nova variável age_bin que assume o valor over50 quando age > 50 e que assume o valor under50 quando age não é >50. Pode agora fazer a tabela de frequências para a nova variável:
# A tibble: 3 × 3
age_bin N Prop
<chr> <int> <dbl>
1 over50 180 0.421
2 under50 245 0.572
3 <NA> 3 0.00701